Can you do Test 4 Section 4 Number 28 please?
Sure! This type of problem seems to be fairly common, at least in the published official tests. If you know that “the minimum value of f appears as a constant or coefficient” whenever a parabola’s equation is written in vertex form, you can sometimes answer the question just by recognizing the form!
Vertex form of a parabola: ![]() , where
, where ![]() is the vertex of the parabola.
is the vertex of the parabola.
In this case, though, you can’t quite do that, because choices C and D both show parabolas in vertex form. So here are a few ways to go:
First, you can recognize from the factored form you’re given that this parabola will have zeros at –6 and 4, which means it will have its vertex right in between them at ![]() . Only choice D is in vertex form and indicates an x-coordinate of –1 at the vertex.
. Only choice D is in vertex form and indicates an x-coordinate of –1 at the vertex.
Second, you can use your graphing calculator to find the minimum, and then look for the choice that has the y-coordinate of the minimum as a constant or coefficient.
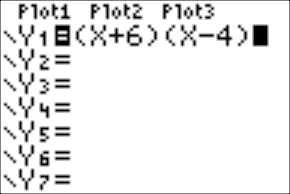




See how the minimum is at (–1, –25)? That means you’re looking for a constant or coefficient of –25, and only choice D has that.
Last, you can complete the square to get into the form you want. In this case, here’s what that looks like:

If you’re paying attention to the differences between the answer choices, you can actually stop as soon as you see that the square you’re completing is ![]() because that’s only contained in choice D. 🙂
because that’s only contained in choice D. 🙂
